LIMIT

Syarira Hanandhita Putri Ilham

XI IPS 3

LIMIT

Dalam matematika , limit adalah nilai yang mendekati suatu fungsi (atau urutan ) ketika masukan (atau indeks) mendekati suatu nilai . Batas sangat penting untuk kalkulus dan analisis matematika , dan digunakan untuk menentukan kontinuitas , turunan , dan integral .

Konsep limit barisan selanjutnya digeneralisasi menjadi konsep limit jaringan topologi , dan terkait erat dengan limit dan limit langsung dalam teori kategori .

Dalam rumus, limit suatu fungsi biasanya ditulis sebagai

\lim _{x\to c}f(x)=L,

a) Limit Fungsi Aljabar

Limit fungsi aljabar terdiri dari jenis bagian yaitu nilai x mendekati satu titik dan nilai x mendekati tak berhingga (∞). Cara penyelesaian nilai x mendekati berhingga adalah dengan substitusi, pemfaktoran, dan dikalikan dengan sekawannya. Sedangkan untuk limit fungsi aljabar di mana x mendekati tak berhingga penyelesainnya yaitu dengan dibagi variabel pangkat tertinggi dan dikalikan sekawan akarnya. Hasil perhitungan dari limit fungsi aljabar tidak boleh 0/0 karena nilainya tidak akan terdefinisi.
1. Strategi Substitusi

Tahapan pertama untuk menyelesaikan suatu limit di satu titik (nilai berhingga) adalah substitusi langsung. Jika dari hasil substitusi langsung tidak diperoleh nilai dengan bentuk tak tentu seperti di bawah ini, maka nilai tersebut adalah menunjukan nilai dari limit yang bersangkutan.
Contoh soal:
2. Strategi Faktorisasi
Apabila hasil substitusi langsung diperoleh nilai bentuk tak tentu, maka kita harus memfaktorkannya sehingga bentuknya menjadi bukan bentuk tak tentu, kemudian kita lanjutkan menggunakan strategi substitusi langsung sehingga diperoleh hasilnya.
Contoh soal:
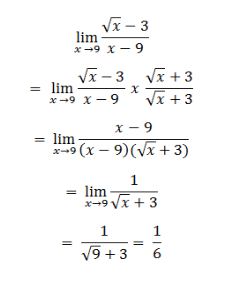
3. Strategi Mengalikan dengan Bentuk Sekawan
Strategi mengalikan dengan bentuk sekawan dilakukan pada limit berbentuk irasional. Hal ini dilakukan jika sebelumnya kita menggunakan strategi substitusi langsung dan strategi faktorisasi, hasil keduanya adalah bentuk tak tentu. Setelah perkalian itu disederhanakan, maka kita menggunakan strategi substitusi langsung lagi, sehingga diperoleh hasilnya.
Contoh soal:

b) Teorema Limit

Misalkan n bilangan asli, k konstanta, serta f dan g fungsi-fungsi yang mempunyai limit di c, maka:

Teorema 1 (T.1) :

lim_{x \to c} k = k

Nilai limit suatu fungsi konstan sama dengan konstanta itu.

Teorema 2 (T.2) :

lim_{x \to c} x = c

Nilai limit suatu fungsi identitas sama dengan nilai pendekatan peubahnya.

Teorema 3 (T.3) :

lim_{x \to c} k f (x) = k lim_{x \to c} f (x)

Limit hasil kali konstanta dengan fungsi sama dengan hasil kali konstanta dengan limit fungsi itu.

Teorema 4 (T.4) :

lim_{x \to c} (f (x) + g (x)) = lim_{x \to c} f (x) + lim_{x \to c} g (x)

Limit jumlah fungsi-fungsi sama dengan jumlah masing-masing limit fungsi.

Teorema 5 (T.5) :

lim_{x \to c} (f (x) - g (x)) = lim_{x \to c} f (x) - lim_{x \to c} g (x)

Limit selisih fungsi-fungsi sama dengan selisih masing-masing limit fungsi.

Teorema 6 (T.6) :

lim_{x \to c} (f (x) g (x)) = lim_{x \to c} f (x) . lim_{x \to c} g (x)

Limit hasil kali fungsi-fungsi sama dengan hasil kali masing-masing limit fungsi.

Teorema 7 (T.7) :

lim_{x \to c} \frac{f (x)}{g (x)} = \frac{lim_{x \to c} f (x)}{lim_{x \to c} g (x)}

, syaratnya g (x) ≠ 0

Limit hasil bagi fungsi-fungsi sama dengan hasil bagi masing-masing limit fungsi dengan syarat limit penyebut tidak sama dengan nol.

Teorema 8 (T.8) :

lim_{x \to c} [f (x)]^{n} = {[lim_{x \to c} f (x)]}^{n}

Limit fungsi pangkat n sama dengan pangkat n dari limit fungsi itu.

Teorema 9 (T.9) :

lim_{x \to c} \sqrt[n]{f (x)} = \sqrt[n]{lim_{x \to c} f (x)}

Limit akar pangkat n dari suatu fungsi sama dengan akar pangkat n dari limit fungsi itu dengan syarat limit fungsi tersebut tidak negatif untuk n bilangan genap.

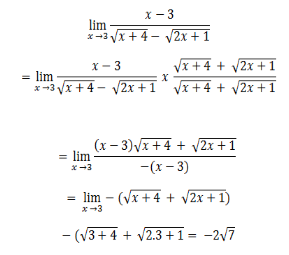
contoh Soal:

Tentukan nilai

lim_{x \to 3} \frac{\sqrt{25 - x^{2}}}{1 + x}

Penyelesaian:

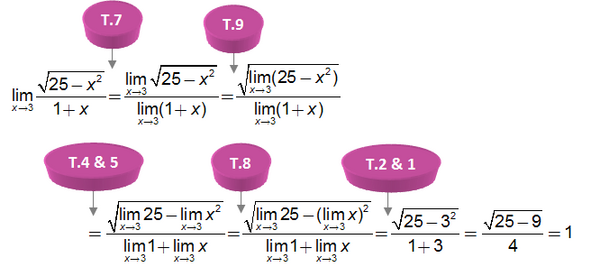
Kamu dapat menentukan nilai limit ini dengan menggunakan teorema limit utama, yaitu sebagai berikut.

c) Limit Tak Tentu

Dalam Matematika, Konsep limit digunakan untuk menjelaskan sifat dari suatu fungsi, saat argumen mendekati ke suatu titik, atau tak hingga atau dari suatu baris saat indeks mendekati tak hingga. Pada Limit terdapat limit bentuk tentu dan limit bentuk tak tentu. Pada postingan kali ini akan diberikan ringkasan padat jelas tentang Limit bentuk tak tentu dan beberapa contoh soal yang dapat muncul waktu Kuis, Ujian dan tes tes lain :)

Macam macam bentuk tak tentu

Cara penyelesaian

Menggunakan : Subtitusi

Perkalian akar sekawan

L’Hopital ( penurunan )