MATRIKS
Syarira Hanandhita Putri Ilham
XI IPS 3
MATRIKS
matriks adalah susunan bilangan-bilangan berbentuk persegi panjang yang diatur dalam baris atau kolom dengan dibatasi kurung. Bilangan yang tersusun dalam matriks disebut elemen/unsur matriks. Baris adalah susunan bilangan-bilangan yang mendatar (horizontal), sedangkan kolom adalah susunan bilangan-bilangan yang tegak (vertikal). Ordo matriks adalah banyaknya elemen baris dan banyaknya elemen kolom dari suatu matriks. Jika sebuah matriks Memiliki i baris dan j kolom, maka matriks tersebut berordo i x j, dapat dituliskan Ai.j.
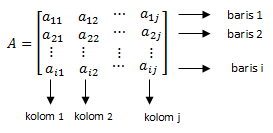
A. Konsep dan Jenis Matriks
- Jenis jenis Matriks berdasarkan pola elemennya
- Matriks identitas adalah matriks persegi yang elemen-elemen diagonal utamanya adalah 1, sedangkan yang lainnya nol.
- Matriks nol adalah matriks yang semua elemennya nol.
- Matriks skalar adalah matriks yang elemen-elemen diagonal utamanya sama, sedangkan elemen lainnya nol.
- Matriks diagonal adalah matriks yang elemen-elemen di luar diagonal utamanya nol.
- Matriks segitiga atas adalah matriks persegi yang elemen-elemen di bawah diagonal utamanya nol.
- Matriks segitiga bawah adalah matriks persegi yang elemen-elemen di atas diagonal utamanya nol.
- Matriks simetri adalah matriks persegi yang elemen-elemen di atas diagonal utamanya sama dengan elemen-elemen di bawah diagonal utamanya.
- Jenis-jenis Matriks berdasarkan jumlah baris dan kolom
- Matriks baris adalah matriks yang hanya terdiri atas satu baris.
- Matriks kolom adalah matriks yang hanya terdiri atas satu kolom.
- Matriks mendatar adalah matriks yang jumlah kolom lebih banyak dari jumlah baris.
- Matriks tegak adalah matriks yang memiliki jumlah baris lebih banyak dari jumlah kolom.
Salah satu fungsi matriks adalah untuk mempermudah perhitungan matematika seperti pada menyelesaikan sistem persamaan linear tiga variabel.
B. Kesamaan Dua Matriks dan Transpose Matriks Serta Operasi Pada Matriks
Persamaan pada dua matriks dapat terjadi apabila memenuhi beberapa syarat ketentuan yang berlaku. Adapun syarat dua buah matriks dinyatakan sama yaitu meliputi:
- Memiliki ordo yang sama.
- Memiliki persamaan pada komponen yang seletak.
Dalam materi persamaan dua matriks mungkin terdapat masalah seperti penyelesaian bentuk aljabar, baik berupa sistem persamaan linear, aljabar sederhana, persamaan kuadrat dan lain lain.
Lambang transpose dari matriks A dapat berupa Aᵀ. Transpose dalam matriks ialah baris yang termasuk di kolom matriks A serta kolomnya termasuk dalam baris matriks A. Dalam transpose tersebut terdapat baris yang ditukar dengan kolom. Hal ini menyebabkan adanya perubahan ordo dalam matriks tersebut. Apabila ordo yang dimiliki matriks A berupa m x n, maka ordo yang dimiliki matriks Aᵀ berupa n x m.
Perubahan ordo juga terdapat dalam matriks A yang bentuknya persegi, tetapi perubahannya tentu berbeda. Dalam matriks persegi hanya ada perubahan komponen saja sehingga ordonya tetap sama. Komponen matriks persegi tidak berubah setelah ditranspose sehingga dapat dinamakan dengan matriks simetris. Untuk itu dapat dinyatakan bahwa jika A = Aᵀ, maka matriks A dapat dinamakan matriks simetris.
Sebuah matriks akan kembali seperti semula apabila pentransposannya dilakukan sebanyak dua kali. Hal ini termasuk dalam sifat dari materi transpose matriks. Di bawah ini merupakan sifat sifat transpose dari matriks yaitu sebagai berikut:
- (Aᵀ)ᵀ = A
- (A + B)ᵀ = Aᵀ + Bᵀ
- (A – B)ᵀ = Aᵀ – Aᵀ
- (kA)ᵀ = kAᵀ, dimana k = konstanta
- (AB)ᵀ = BᵀAᵀ
- Penjumlahan dan Pengurangan Matriks
Contoh :

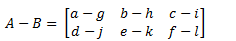
- Perkalian Skalar pada Matriks
Contoh :
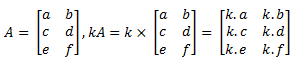
- Perkalian Dua Matriks
Bentuk perkalian antar matriks secara umum, yaitu :
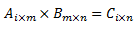
Untuk mencari hasil kali matriks A dengan matriks B ialah dengan mengalikan elemen pada baris-baris matriks A dengan elemen pada kolom-kolom matriks B, kemudian jumlahkan hasil perkalian antara baris dan kolom tersebut.
Contoh matriks :
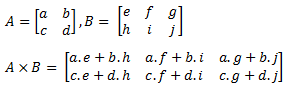
- Transpose Matriks
Contoh :
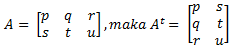
C. Menyelesaikan Masalah Kontekstual pada Matriks
1. Diketahui sebuah matriks
maka hasil perhitungan dari x+2xy+y = …..
Untuk mengerjakan soal ini, Anda harus memahami sifat-sifat dan operasi perhitungan matriks untuk memudahkan Anda dalam proses penyelesaian soal tersebut.
Pertama, Anda harus menulis bentuk F+A-C seperti di bawah ini.
Dari bentuk matriks di atas, Anda dapat membentuk sebuah persamaan sesuai dengan baris dan kolom pada kedua ruas seperti 6+x = 8.
Dari persamaan ini, didapatkan nilai x=2. Kemudian Anda dapat memasukkan nilai tersebut pada persamaan 2 – y = -x atau y+6 = 5x. Sehingga di dapatkan nilai y adalah 4.
Anda dapat memasukkan nilai x dan y ke dalam persamaan x+2xy+y. Sehingga di dapatkan 2+2.2.4+4 = 22. Sehingga jawaban dari persamaan tersebut adalah 22.
2. Diketahui sebuah matriks
Jika X+Y = M. Maka tentukan nilai a+b = …
Sama seperti soal sebelumnya, Anda harus menambahkan kedua matriks mengikuti persamaan yang diberikan seperti berikut ini.
Dari hubungan matriks pada kedua ruas memiliki posisi yang sama, maka Anda dapat secara langsung membentuk sebuah persamaan 2 + 3a = 8, sehingga di dapatkan nilai a = 2.
Hal ini juga Anda lakukan pada persamaan -2b – 2 = 10, sehingga nilai b = -6. Maka hasil a+b adalah 2 + (-6) = -4.
3. Diketahui suatu persamaan matriks berikut
Tentukan nilai 3x – 2y = ….
Untuk mengerjakan soal ini, Anda harus mengalikan angka 3 pada matriks pertama sehingga di dapatkan hasil
Hasil matriks ini kemudian Anda tambahkan dengan matriks kedua untuk mendapatkan hasil akhir seperti di ruas kanan.
Anda dapat menambahkan baris dan kolom yang sama pada kedua matriks di ruas kiri seperti di bawah ini.
4x – 4 = 8, sehingga didapatkan nilai x = 3.
2y + 3 = 13, sehingga didapatkan nilai y = 5.
Maka nilai 3x – 2y adalah 3(3) – 2(5) = -1
4. Diketahui suatu persamaan matriks tidak lengkap berikut.
Carilah hasil dari 2a + b – 2c + d = …..
Langkah mengerjakan soal di atas, mirip dengan soal sebelumnya. Anda dapat mengalikan angka 2 dengan matriks pertama sehingga di dapatkan
Anda dapat membuat persamaan setara antara ruas kanan dan kiri seperti penyelesaian di bawah ini.
Anda perlu melakukan perkalian pada ruas kiri. Sehingga didapatkan bentuk yang sama antara matriks ruas kanan dan ruas kiri seperti di bawah ini.
Dari persamaan di atas, ruas kanan dan ruas kiri sudah setara sehingga Anda dapat mencari nilai a, b, c, dan d.
2a+4 = 8, maka nilai a = 2
-6 = 2c + 4, maka nilai c = -5
3 = 3d + 6, maka nilai d = -1
2 + b = cd + 12, maka nilai b = 15
Sehingga nilai dari 2a + b – 2c + d = 2.2 + 15 – 2(-5) + (-1) = 28
5. Diketahui matriks
jika C.O = A, Tentukan nilai det A
Untuk mengerjakan soal ini, Anda harus memahami konsep determinan matriks. Sifat determinan matriks menyatakan bahwa jika CO = A, maka det(C) x det(O) = det(A). Sehingga, untuk menentukan det(A), Anda cukup mencari nilai det(C) dan det(O).
det(C) = 2(6) – 4(5) = -8, det(O) = -1(2) – 1(0) = -2, sehingga det(A) = -8 x -2 = 16.
Jadi, nilai determinan matriks A adalah 16.
6. Misalkan terdapat matriks
- Tentukan hasil operasi perkalian matriks tersebut.
- Tentukan At.
- Tentukan det (B).
- Tentukan B-1.
DAFTAR PUSTAKA
https://idschool.net/sma/pengertian-dan-jenis-jenis-matriks/
http://www.antotunggal.com/2021/09/rangkuman-materi-kesamaan-dua-matriks-dan-transpose-matriks.html
https://rumuspintar.com/matriks/


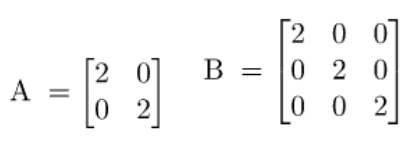

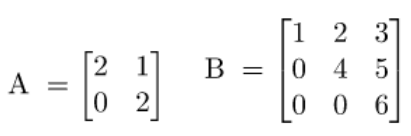
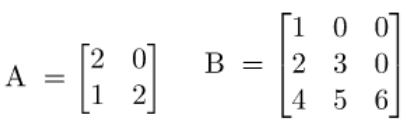

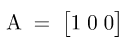





















Komentar
Posting Komentar