LUAS SEGITIGA DENGAN TRIGONOMETRI, ATURAN SINUS DAN ATURAN COSINUS

 Syarira Hanandhita Putri Ilham

 X IPS 1

 Matematika wajib



LUAS SEGITIGA DENGAN TRIGONOMETRI, ATURAN SINUS DAN ATURAN COSINUS



  • Luas segitiga dengan Trigonometri
Pada umumnya, luas suatu segitiga dapat diperoleh dengan mengalikan alas dan tinggi dari segitiga tersebut dan kemudian membaginya dengan 2. Namun, terdapat cara lain untuk menghitung luas segitiga yakni dengan menggunakan rumus aturan trigonometri.

Sebagaimana telah kita pelajari bahwa luas suatu segitiga dapat diperoleh dengan mengalikan alas dan tinggi dari segitiga tersebut dan kemudian membaginya dengan 2, atau dapat dituliskan sebagai

Selain menggunakan rumus di atas, luas segitiga tersebut juga dapat diperoleh dengan menggunakan rumus aturan trigonometri. Untuk penjelasannya, amatilah segitiga ABC berikut!

Gambar 1. Segitiga ABC dengan sudut dan sisi-sisinya

Perhatikan bahwa segitiga ABC pada Gambar 1 terbagi lagi menjadi dua segitiga yakni ΔADCΔADC dan ΔBDCΔBDC. Pada ΔADCΔADC, kita peroleh

Dengan demikian,

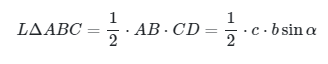
Jadi, luas LΔABCLΔABC dapat dinyatakan sebagai

Dengan cara yang sama, untuk setiap segitiga ABC juga berlaku:

Contoh Soal dan Pembahasannya 



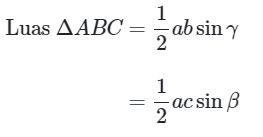
Contoh 1:

Tentukan luas segitiga ABC pada Gambar 1 di atas jika diketahui sisi BC=4BC=4 cm, AC=7√3AC=73 cm dan ∠C=600∠C=600.

Pembahasan:

Diketahui BC=a=4BC=a=4 cm; AC=b=7√3AC=b=73 dan ∠C=600∠C=600. Dengan demikian,  


Contoh 2:

Sebuah segitiga ABC diketahui luasnya 18 cm2. Jika panjang sisi BC=4BC=4 cm dan AB=6√3AB=63 cm, maka tentukanlah besar sudut B.

Pembahasan:

Diketahui luas segitiga = 18, BC=a=4BC=a=4; dan AB=c=6√3AB=c=63. Dengan demikian, kita


Luas Segitiga Jika Hanya Diketahui Panjang Ketiga Sisinya

Dari Gambar 1, jika diketahui hanya nilai ketiga sisinya maka luas segitiga ABC dapat juga ditentukan dengan rumus berikut.

di mana: S=12(a+b+c)S=12(a+b+c).

Bukti:
Menurut identitas trigonometri diketahui bahwa


Jika persamaan (2) disubstitusikan ke (1) maka diperoleh:

di mana: S=12(a+b+c)S=12(a+b+c).



Contoh 3:

Hitunglah luas segitiga ABC jika diketahui panjang sisi-sisinya a = 16 cm, b = 14 cm, dan c = 10 cm!

Pembahasan:

Pertama, kita hitung



Sehingga luas segitiga ABC adalah



Jadi, luas segitiga ABC adalah 40√3 cm2.


  • Aturan Sinus


Aturan sinus adalah perbandingan antara setiap sisi dan sinus sudut di depan sisi tersebut memiliki nilai yang sama. Aturan sinus ini berlaku pada segitiga, baik segitiga siku-siku maupun segitiga sembarang.

Misalnya pada segitiga ABC yang memiliki panjang sisi a, b, dan c, serta sudut A, B, C, maka aturan sinus yang berlaku adalah sebagai berikut.



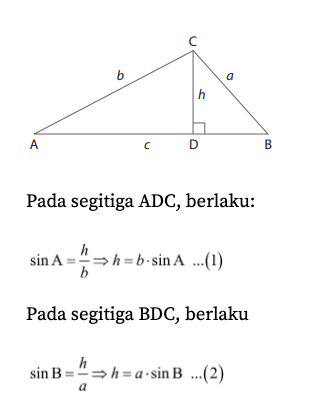
Substitusikan nilai h pada persamaan (1) ke ke persamaan (2).

Langkah di atas juga berlaku saat kamu akan mencari nilai c. Dengan demikian, aturan sinusnya menjadi seperti berikut.

Aturan sinus bisa digunakan pada dua pasang sudut sisi yang saling berhadapan, di mana salah satunya tidak diketahui.

Untuk lebih jelasnya, simak contoh soal berikut.

Contoh Soal dan Pembahasannya

Contoh Soal 1:

Pada awalnya, Menara Pisa dibangun dengan ketinggian 56 m. Ternyata, tanah di lokasi pembangunan menara rentan akan kerapuhan, sehingga terjadi kemiringan. Pada jarak 44 m dari dasar menara diperoleh sudut elevasi 55o, tentukan derajat kemiringan menara dari posisi awalnya!

Pembahasan:

Jika digambarkan akan menjadi seperti berikut.

Persoalan di atas bisa disederhanakan menjadi segitiga berikut.

Gunakan aturan sinus untuk menyelesaikan masalah di atas.

Dengan demikian, besar sudut A = 180o – (B + C)  atau sudut A = 85o

Jadi, derajat kemiringan Menara Pisa adalah x = 90o – 85o = 5o.

Contoh soal 2:

 Andi sedang mengukur mainan segitiganya yang tiap sudutnya dikodekan dengan A, B, dan C, kemudian diketahui segitiga tersebut memiliki sudut A = 30º, sisi a = 6cm dan sisi b = 8cm. Hitung besar sudut B!

Pembahasan

Akan dicari besar sudut B

sin B = (b sin A)/a  

sin B = 8/6 sin 30̊

sin B = 2/3

B = arc sin B

B = arc sin (2/3)

B = 41,8̊

Jadi, besar sudut B adalah 41,8̊ atau 180̊ – 41,8̊ = 138,2̊

Contoh Soal 3:

 Sebuah segitiga ABC memiliki panjang AC = 4 cm. Jika besar ∠ ABC = 60o dan ∠BAC = 30o, maka panjang BC = … cm.

Pembahasan

AC/sin ∠ABC = BC/sin∠BAC

4cm/sin 60 = BC/sin30

4cm/½√3 = BC/½

BC = ½ × 4cm/½√3

BC = 4cm/√3

BC = 4/3 √3 cm

Jadi, panjang BC adalah BC4/3 √3cm.

Contoh soal 4:

Diketahui sebuah segitiga ABC dengan panjang AB = 9cm dan BC = 12cm. Jika besar ∠ ABC = 30o, tentukan luas segitiga ABC!

Pembahasan

L = ½ a t

  • Misal a = AB, maka t adalah garis tegak lurus AB ke titik C berhadapan dengan ∠ ABC, maka

Sin ∠ABC = t/BC

t = BC × Sin ∠ABC

Sehingga diperoleh

L = ½ a t

L = ½ × AB × BC × Sin ∠ABC

L = ½ × 9cm × 12cm × Sin 30o

L = ½ × 9cm × 12cm × ½

L = 27cm2

  • Misal a = BC, maka t adalah garis tegak lurus BC ke titik A berhadapan dengan ∠ ABC, maka

Sin ∠ABC = t/AB

t = AB × Sin ∠ABC

Sehingga diperoleh

L = ½ a t

L = ½ × BC × AB × Sin ∠ABC

L = ½ × 12cm × 9cm × Sin 30o

L = ½ × 12cm × 9cm × ½

L = 27cm2

Jadi,  luas segitiga ABC adalah 27cm2.

Contoh Soal 5:

Diketahui sebuah segitiga PQR memiliki luas sebesar 96cm2. Jika panjang PR = 12cm dan besar ∠PRQ = 60o, tentukan panjang QR!

Pembahasan

L = ½ × PR × QR × Sin ∠PRQ

96cm2 = ½ × 12cm × QR × Sin 60o

96cm2 = ½ × 12cm × QR × ½√3

96cm2 = 4√3cm × QR

QR = 96cm2 ÷ 4√3cm

QR = 24/√3 cm

QR = 8√3cm

Jadi, panjang QR adalah 8√3cm.

  • Aturan Cosinus

Aturan kosinus adalah hubungan antara panjang sisi segitiga dan nilai kosinus dari salah satu sudut yang ada di dalam segitiga tersebut. Untuk mencari tahu persamaan yang berlaku di aturan kosinus, perhatikan gambar berikut.

Pada segitiga ADC, berlaku:

h2 = b2 – AD2…(1)

Pada segitiga siku-siku BDC, berlaku:

h2 = a2 – BD2…(2)

Substitusikan nilai h2 pada persamaan (1) ke persamaan (2), diperoleh:

b2 – AD2 = a2 – BD2

Oleh karena BD = c – AD, maka:

b2 – AD2 = a2 – (c – AD)2

b2 – AD2 = a2 – c2 + 2.c.AD – AD2

a2 = b2 + c2 – 2.c.AD

 Pada segitiga ADC berlaku AD = b. cos A, sehingga dapat dinyatakan sebagai berikut.

a2 = b2 + c2 – 2.b.c.cos A

Dari perhitungan di atas, aturan kosinus memenuhi persamaan berikut.

Contoh Soal dan Pembahasannya

Contoh soal 1:

Kapal laut A dan B berlayar dari titik M pada waktu yang bersamaan. Kapal A berlayar dengan jurusan tiga angka 102o dan kapal B berlayar dengan jurusan tiga angka 232o. Jika kecepatan kapal A 30 km/jam dan kecepatan kapal B 45 km/jam, tentukan jarak kedua kapal tersebut setelah berlayar selama 3 jam!

Pembahasan:

Untuk memudahkan Quipperian dalam menyelesaikan soal tersebut, perhatikan ilustrasi berikut.

Oleh karena kecepatan A = 30 km/jam, maka setelah 3 jam jarak yang ditempuh adalah 90 km. Untuk B, jarak yang ditempuh selama 3 jam adalah 135 km. Di sisi lain, besaran sudut AMB = 232o -102o = 130o. Berdasarkan aturan kosinus, diperoleh:

AB2 = AM2 + BM2 – 2.AM.BM.cos M

AB2 = 902 + 1352 – 2.90.135.cos 130o

AB = 204,8 km

Jadi, jarak kedua kapal tersebut setelah berlayar selama 3 jam adalah 204,8 km.

Contoh soal 2:

Diketahui sebuah segitiga ABC memiliki sisi dengan panjang

a = 10 cm

c = 12 cm

besar sudut B = 60̊.

Hitung panjang sisi b!

Pembahasan

b2 = a2+ c2 – 2ac cos B

b2 = 100+144 – 44 cos 60̊

b2 = 244 – 44(0,5)

b2 = 244 – 22

b2 = 222

b = 14,8997

Jadi, panjang sisi b adalah 14,8997 cm







DAFTAR PUSTAKA

Komentar

Posting Komentar

Postingan populer dari blog ini

Lucy Guo: Dari Anak Jenius Hingga Miliarder Teknologi

Gambar
Lucy Guo: Dari Anak Jenius Hingga Miliarder Teknologi Syarira Hanandhita Putri Ilham, 20240101256 28 September 2025  00.15                                               ( FOTO: Credit to The Indian Express) Perjalanan Hidup   Lucy Guo lahir pada tahun 1994 di California, Amerika Serikat, sebagai anak dari keluarga imigran Tionghoa. Sejak kecil ia sudah menunjukkan ketertarikan terhadap teknologi, belajar pemrograman secara mandiri dan mencari cara menghasilkan uang dari ide-ide kecil seperti menjual barang koleksi. Ia kemudian masuk ke Carnegie Mellon University untuk mendalami Ilmu Komputer, tetapi di tengah jalan memutuskan untuk keluar setelah mendapat kesempatan mengikuti Thiel Fellowship, sebuah program beasiswa bagi wirausahawan muda.  Setelah keluar dari kampus, Lucy mengambil berbagai posisi di perusahaan-perusahaan teknologi seperti Facebook, Snapchat, da...
Baca selengkapnya

LUAS SEGI-n BERATURAN, JARI-JARI LINGKARAN LUAR DAN LINGKARAN DALAM SEGITIGA, GARIS SINGGUNG PERSEKUTUAN LUAR/DALAM LINGKARAN

Gambar
  SYARIRA HANANDHITA PUTRI ILHAM  X IPS 1  MATEMATIKA WAJIB LUAS SEGI-n BERATURAN, JARI-JARI LINGKARAN LUAR DAN LINGKARAN DALAM SEGITIGA, GARIS SINGGUNG PERSEKUTUAN LUAR/DALAM LINGKARAN Luas Segi-n Beraturan Segi n beraturan pada umumnya terbagi menjadi beberapa jenis seperti segitiga, segiempat, segi lima, segi enam, seni tujuh, segi delapan dan sebagainya. Segi n beraturan ini memiliki rumus yang berbeda-beda. Bagaimana rumus segi n beraturan itu? Bangun datar segi n beraturan pada umumnya berasal dari lingkaran yang dibagi menjadi beberapa bagian yang besarnya sama sehingga bentuknya menyerupai segitiga sama kaki. Segi n beraturan memang berasal dari bagian-bagian kecil pada lingkaran. Untuk itu rumus segi n beraturan melibatkan jari jari dan sudut pusat di dalamnya. Sudut pusat ialah sudut segitiga (dinyatakan dalam tanda sudut berwarna merah) yang memiliki besar 360°/n. Selain itu dalam bangun datar segi n beraturan terdapat sisi yang dinyatakan dalam bentuk x. Untuk...
Baca selengkapnya

REVIEW SERIAL "DARK": SERIAL NETFLIX TERBAIK YANG UNDERRATED

Gambar
  DARK Serial Dark pertama kali dirilis pada tahun 2017, disusul dua musim berikutnya pada 2019 dan 2020, hasil garapan Baran bo Odar dan Jantje Friese, bukan sekadar kisah misteri anak hilang biasa. Serial Netflix asal Jerman ini membawa penonton berkelana menembus waktu, menggabungkan ilmu pengetahuan, filsafat, dan ketegangan ke dalam misteri yang kompleks, serta mengungkap rahasia kelam empat keluarga di kota fiktif Winden, dan bergulat dengan paradoks yang rumit. Dengan alur cerita yang memutar balik waktu, karakter yang mendalam, dan penggarapan visual yang cermat, "Dark" menciptakan pengalaman menonton yang luar biasa dan penuh teka-teki. Membuat serial ini menjadi salah satu serial garapan Netflix terbaik dengan ide cerita yang gila. Saya sangat menyukai seluruh aspek yang ada di dalamnya dan semuanya sangat mengagumkan bagi saya. Saya menyukai sinematografinya, scoring-nya, seluruh rangkaian plot ceritanya, dan seluruh karakternya. Saya juga menyukai tema ...
Baca selengkapnya