KOMPOSISI FUNGSI DAN INVERS FUNGSI

Desember 09, 2021

SYARIRA HANANDHITA PUTRI ILHAM

X IPS 1

KOMPOSISI FUNGSI DAN INVERS FUNGSI BESERTA CONTOH SOALNYA

Fungsi Komposisi

Fungsi komposisi merupakan susunan dari beberapa fungsi yang terhubung dan bekerja sama.

Sebagai ilustrasi jika fungsi f dan g adalah mesin yang bekerja beriringan. Fungsi f menerima input berupa (x) yang akan diolah di mesin f dan menghasilkan output berupa $f(x)$ . Kemudian $f(x)$ dijadikan input untuk diproses di mesin g sehingga didapat output berupa $g(f(x))$ .

Ilustrasi tersebut jika dibuat dalam fungsi merupakan komposisi g dan f yang dinyatakan dengan $g o f$ sehingga:

$(g o f)(x) = g(f(x))$

dengan syarat: $R_f \cap D_g \not= {\O}$ .

fungsi komposisi

Komposisi bisa lebih dari dua fungsi jika $f:A \rightarrow B$ , $g:B \rightarrow C$ , dan $h:C \rightarrow D$ , maka $h o g o f:A \rightarrow D$ dan dinyatakan dengan:

$(h o g o f)(x) = h(g(f(x)))$

Sifat-sifat fungsi komposisi:

Operasi pada fungsi komposisi tidak besifat komutatif $(g o f)(x) \not= (f o g)(x)$

Operasi bersifat asosiatif: $(h o g o f)(x) = (h o(g o f))(x) = ((h o g) o f)(x)$

Contoh:

Jika $f(x) = 2x + 3$ dan $(f o g)(x) = 2x^2 + 6x - 7$ , maka g(x) adalah

$(f)(g(x)) = 2x^2 + 6x - 7$

$2(g(x)) + 3 = 2x^2 + 6x - 7$

$g(x) = x^2 + 3x - 5$

Fungsi Invers

Jika fungsi $f:A \rightarrow B$ memiliki relasi dengan fungsi $g:B \rightarrow A$ , maka fungsi g merupakan invers dari f dan ditulis $f^{-1}$ atau $g = f^{-1}$ . Jika $f^{-1}$ dalam bentuk fungsi, maka $f^{-1}$ disebut fungsi invers.

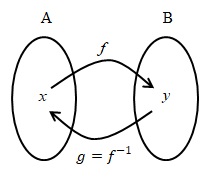
fungsi invers

Menentukan Invers

Menentukan invers suatu fungsi $y = f(x)$ dapat ditempuh dengan cara berikut:

Ubah persamaan $y = f(x)$ ke dalam bentuk $x = f(y)$

Gantikan x dengan $f^{-1}(y)$ sehingga $f(y) = f^{-1}(y)$

Gantikan y dengan x sehingga diperoleh invers berupa $f^{-1}$

Contoh:

Menentukan invers dari $=x^2 - 2x + 4$ :

$y = [x^2 - 2x + 4$

$y = (x - 1)^2 + 3$

$(x - 1)^2 = y - 3$

$x - 1 = \pm \sqrt{y - 3}$

$x = \pm \sqrt{y -3 + 3}$

Sehingga inversnya adalah

$f^{-1}(x) =\pm \sqrt{y - 3 + 1}$ dan bukan merupakan fungsi karena memiliki dua nilai.

Rumus Fungsi Invers

JENIS FUNGSI	f(x)	$f^{-1}(x)$
Fungsi linier	$f(x) = ax + b$	$f^{-1}(x) = \frac{x-b}{a}$
Fungsi pecahan linier	$f(x) =\frac{ax+b}{cx+d}$	$f^{-1}(x) = \frac{-dx+b}{cx-a}$
Fungsi Irrasional	$f(x) =\sqrt[n]{ax+b}$	$f^{-1}(x) = \frac{x^n-b }{a}$
Fungsi eksponen	$f(x) = a^x$	$f^{-1}(x) = ^a\log x$
Fungsi logaritma	$f(x) = ^a\log x$	$f^{-1}(x) = a^x$

Contoh

JENIS FUNGSI	$f(x)$	$f^{-1}(x)$
Fungsi linier	$f(x) = 2x+3$	$f^{-1}(x) = \frac{x-3}{2}$
Fungsi pecahan linier	$f(x) = \frac{2x+3}{4x+5}$	$f^{-1}(x) = \frac{-5x+3}{4x-2}$
Fungsi Irrasional	$f(x) = \sqrt[4]{2x+3}$	$f^{-1}(x) = \frac{x^4-3}{2}$
Fungsi eksponen	$f(x) = 2^x$	$f^{-1}(x) = ^2\log x$
Fungsi logaritma	$f(x) = ^2\log x$	$f^{-1} = 2^x$