TURUNAN FUNGSI ALJABAR
Syarira Hanandhita Putri Ilham
XI IPS 3
a) Turunan Fungsi Aljabar dan Rumus Rumus Turunan
Turunan fungsi atau juga bisa disebut dengan diferensial adalah fungsi lain dari suatu fungsi sebelumnya, contohnya fungsi f dijadikan f' yang mempunyai nilai tidak memakai aturan dan hasil dari fungsi akan berubah sesuai dengan variabel yang dimasukan, atau secara umum suatu besaran yang berubah seiring perubahan besaran lainnya. Proses dalam menemukan turunan disebut sebagai diferensiasi. Lalu untuk pengertian turunan aljabar adalah perluasan dari materi limit fungsi.
Notasi turunan fungsi aljabar seperti berikut:
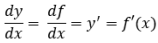
Seperti yang telah disebutkan di atas, jika turunan fungsi aljabar merupakan perluasan dari materi limit fungsi sehingga dapat didefinisikan seperti berikut:
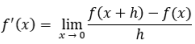
Rumus Turunan Aljabar
Setelah memahami tentang pengertian dari turunan fungsi aljabar, hal yang perlu Sobat Pintar pelajari adalah rumus dari turunan fungsi aljabar. Rumus turunan fungsi aljabar ini terbagi menjadi beberapa rumus berikut:
Turunan Fungsi PangkatBentuk dari fungsi kali adalah f(x) = u(x) . v(x), sehingga turunannya adalah f’(x) = u’(x)v(x) + u(x)v’(x).
Contoh Soal:


Contoh Soal:

b) Persamaan Garis Singgung Kurva Menggunakan Turunan
Ilustrasi untuk persamaan garis singgung pada kurva y = f(x) bisa digambarkan sebagai berikut

Nilai x1 = absis sedangkan y1 adalah ordinat. Hubungan antara absis dengan ordinat bisa dinyatakan dengan persamaan kurva, yaitu
y1 = f(x1)
Kemiringan garis (gradien =m) bisa dinyatakan dengan turunan y=f(x) di x1
m = f ‘(x1)
Selanjutnya persamaan garis singgung dengan gradien m dan melalui (x1, y1) bisa dinyatakan dengan
y — y1 = m(x — x1)
Contoh soal 1Tentukan persamaan garis singgung pada kurva y = x4 — 3x3 + 6x + 7 di titik yang berabsis 2
Jawab :
x = 2
y = x4 — 3x3 + 6x + 7
y = 24 — 3.23 + 6.2 + 7 = 16 — 24 + 12 + 7 = 11
m = y’ = 4x3 — 9x2 + 6 = 4.23 — 9.22 + 6 = 32 — 36 + 6 = 2
y — y1 = m(x — x1)
y — 11 = 2 (x — 2)
y — 11 = 2x — 4
y = 2x + 7
Contoh Soal 2
Tentukan persamaan garis singgung pada kurva y = 2x3 — 24 di titik yang berordinat 30
Jawab :y = 30
2x3 — 24 = 30
2x3 = 54
x3 = 27
x = 3
m = y’ = 6x2 = 6.32 = 54
y — y1 = m(x — x1)
y — 30 = 54 (x — 3)
y — 30 = 54x — 162
y = 54x — 132
Contoh Soal 3
Persamaan garis singgung pada kurva y = 20 — x4 yang bergradien 32 adalah …
Jawab :m = 32
y’ = 32
-4x3 = 32
x3 = -8
x = -2
y = 20 — x4 = 20 -(16) = 4
y — y1 = m(x — x1)
y — 4 = 32(x + 2)
y — 4 = 32x + 64
y = 32x + 68
c) Masalah Kontekstual Menggunakan Turunan Satu dan Turunan 2 Serta Titik Stasioner dari Kurva
Apa Itu Titik Stasioner?
Titik stasioner merupakan sebuah titik dalam grafik yang turunan kurva pertamanya sama dengan nol. Titik ini disimbolkan dengan rumus berikut:
Supaya lebih mudah dipahami, titik stasioner dapat digambarkan dalam garis fungsi seperti gambar di bawah ini.
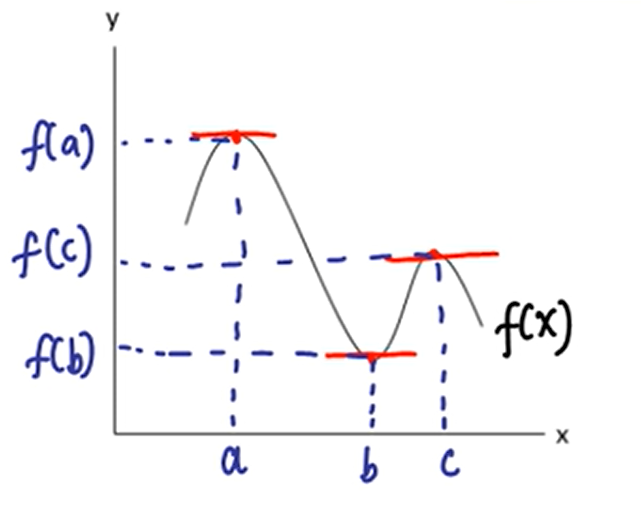
Pada garis fungsi ini, bisa menemukan tiga titik. Pertama, pada saat nilai x=a, sehingga fungsinya disebut sebagai f(a). Kemudian, titik stasioner selanjutnya muncul saat nilai x=b, fungsinya disebut sebagai f(b). Lalu yang terakhir muncul saat nilai x=c, sehingga fungsinya adalah f(c).
Oleh karena itu, titik stasionernya adalah:
- (a, f(a))
- (b, f(b))
- (c, f(c))
juga bisa menyebut bahwa nilai stasionernya adalah:
- f(a)
- f(b)
- f(c)
Cara Menentukan Titik Stasioner
Lalu, bagaimana cara menentukan titik stasioner? Coba ikuti contoh soal berikut.
Tentukan titik stasioner fungsi berikut:
Ingat, nilai fungsi dari titik stasioner harus sama dengan nol (f’(x)=0). Sehingga, turunan dari fungsi ini adalah:
Sehingga, mendapatkan nilai x:
Sekarang, hanya perlu menentukan nilai f(x) untuk mendapatkan titik stasioner dengan memasukkan nilai x. Pertama, harus mencari nilai fungsi f(-3).
Berarti pada fungsi f(-3), titik stasioner ada pada titik (-3,31).
Selanjutnya, cari nilai fungsi f(1).
Artinya, pada fungsi f(1), titik stasioner ada pada titik (1,-1).
Salah satu nilai stasioner pada grafik berikut ini adalah ….
a. 5
b. 6
c. 4 ½
d. 4
e. 1 ½
Nilai stasioner adalah nilai y dari titik stasioner. Dari gambar, dapat dilihat bahwa titik-titik stasionernya adalah (1,6), (4,½), dan (6,3½). Jadi, nilai stasionernya adalah 6, ½, dan 3½. Pada pilihan jawaban yang tersedia, jawaban yang benar adalah b. 6.
DAFTAR PUSTAKA
https://supermatematika.com/persamaan-garis-singgung-dengan-turunan




Komentar
Posting Komentar